Не будет большим преувеличением сказать, что рынок средств статического тестирования защищенности приложений (Static Application Security Testing, SAST) в наше время переживает самый настоящий бум. Не проходит и пары месяцев между публикациями очередных научных работ на эту тему, ежегодно на рынок выводятся все новые и новые инструменты статического анализа защищенности, а месту SAST в процессе разработки ПО отводятся целые секции на международных ИБ-конференциях. В условиях непрерывного информационного прессинга со стороны поставщиков инструментария SAST, нелегко разобраться в том, что есть правда, а что − не более, чем маркетинговые уловки, слабо коррелирующие с действительностью. Давайте попробуем понять, что же действительно под силу инструментам SAST и как быть с тем, что им «не по зубам». Для этого нам придется немного погрузиться в теорию, лежащую в основе современных средств статического анализа защищенности кода.
Тьюринг, Райс - вот эти вот все
TL/DR: задача статического тестирования защищенности программ алгоритмически неразрешима.
Представьте себе множество полностью абстрактных программ P, которые только и умеют, что зависать на одних наборах входных данных и останавливаться через некоторое число операций на других. Очевидно, что класс P охватывает любые теоретически возможные программы, поскольку это свойство можно приписать любой из них.
Теперь представьте, что одна из таких программ (назовем ее h) является анализатором, умеющим отвечать на простой вопрос: зависает ли произвольная программа p из множества P на заданном наборе данных n? Очевидно, что отвечать на этот вопрос h сможет только завершая свою работу и тем самым сообщая, что p зависает на n. Иными словами, если p(n) не останавливается, то h(p(n)) должна завершить свою работу за конечное число шагов, а если p(n) останавливается, то h(p(n)) должна зависнуть.
Ну, а теперь представьте, что произойдет, если мы попробуем ответить с помощью такого анализатора на вопрос: зависнет ли он сам, в результате анализа самого себя, анализирующего самого себя (ведь p может быть любой программой из P, значит она может быть и самой h)? В этом случае получается, что если h(h(n)) остановится, то анализ h(n) зависает, а если h(h(n))) зависает, то анализ h(n) останавливается. Но ведь h как раз и есть h(n), а, следовательно, мы здесь имеем противоречие и анализатор подобный h не имеет права на существование.
Описанное является вольным изложением доказательства Теоремы останова, сформулированной Алланом Тьюрингом (основоположником современной теоретической информатики) в далеком 1936-м. Данная теорема утверждает, что не существует такой программы, которая могла бы проанализировать другую программу и ответить на вопрос, остановится ли та на заданном наборе входных данных. Хорошо, но можем ли мы построить такую программу, которая дает ответ на вопрос о каких-либо других свойствах программ?
Поскольку множество P включает в себя все возможные программы, мы всегда можем разбить его на два класса (пусть будут A и B) по признаку наличия у программ любого нетривиального инвариантного свойства. Под нетривиальным инвариантным свойством подразумевается такое свойство, которым любая программа множества P либо обладает, либо не обладает и при этом все функционально тождественные программы (дающие одни и те же наборы данных на выходе при одинаковых наборах данных на входе) либо все вместе обладают этим свойством, либо все вместе не обладают.
Давайте представим, что есть некоторый анализатор q, который принимает на вход произвольную программу p множества P и останавливается, если p относится к одному из классов. Пусть, для определенности, это будет класс A. Пусть pa - программа, относящаяся к классу A и зацикливающаяся на любом входе. Выберем также из класса B произвольную программу pb. Для каждой программы p определим программу p’, получающую на вход данные x и выполняющую следующий алгоритм:
- p(p)
- pb(x)
Теперь построим программу q’, которая получает на вход произвольную программу p, строит для нее p’ и вычисляет q(p’).
Если p’ зависает на первом шаге, значит p’ функционально тождественна pa (и относится к классу A), а, следовательно, q’ должна немедленно остановиться. Если p’ проходит первый шаг, то p’ функционально тождественна pb (и относится к классу B), а, следовательно, q’ должна зависнуть. Таким образом, для любой программы p, q’(p) останавливается тогда, когда p(p) не останавливается. Но в роли p может оказаться и сама q’, следовательно, p(p) останавливается только тогда, когда p(p) не останавливается. Снова пришли к противоречию.
Утверждение о том, что не существует такой программы, которая могла бы давать ответ на вопрос о наличии любых нетривиальных инвариантных свойств у произвольно взятой программы, доказал ученый Генри Райс в 1953 году. Фактически, его работа обобщает Теорему останова, поскольку свойство останавливаться на заданном наборе данных является нетривиальным и инвариантным. Теорема Райса имеет бесконечное множество практических значений, в зависимости от рассматриваемых свойств: «невозможно с помощью программы классифицировать алгоритм, реализуемый другой программой», «невозможно с помощью программы доказать, что две других программы реализуют один и тот же алгоритм», «невозможно с помощью программы доказать, что другая программа на любых наборах данных не входит в какие-либо состояния…» и т.п. И вот на последнем примере стоит остановиться подробнее.
В момент выполнения любого (как абстрактного, так и реального) алгоритма некоей универсальной выполняющей программой (например, виртуальной машиной, эмулирующей полноценный компьютер с установленной ОС), можно взять снимок этой машины, включая состояние самой выполняемой программы в адресном пространстве машины и ее внешнего окружения, такого, как дисковые накопители, состояние внешних устройств и т.п. и позднее, восстановив его, продолжить выполнение программы с того же самого места. По сути, весь процесс выполнения любой программы, представляет собой череду сменяющихся состояний, последовательность которых как раз и определяется ее кодом. При этом, в случае наличия каких-либо ошибок в конфигурации или реализации, как самой программы, так и выполняющей ее машины, велика вероятность того, что процесс выполнения войдет в состояние, которое изначально не предполагалось разработчиками.
А что есть уязвимость? Это возможность с помощью входных данных заставить процесс выполнения войти в такое состояние, которое приведет к реализации какой-либо из угроз в отношении обрабатываемой процессом информации. Следовательно, можно определить свойство защищенности любой программы, как ее способность в каждый момент времени оставаться, вне зависимости от изначальных входных данных, в рамках заранее определенного множества допустимых состояний, определяющего политику ее безопасности. При этом, задача анализа защищенности программы очевидно сводится к анализу невозможности ее перехода в любое неразрешенное политикой безопасности состояние на произвольном наборе входных данных. То есть, к той самой задаче, алгоритмическая неразрешимость которой была давным-давно доказана Генри Райсом.
Так получается, что же… весь рынок инструментария SAST – это индустрия обмана? В теории – да, на практике же, всё как обычно - возможны варианты.
Теория SAST на практике
Даже оставаясь в теоретическом поле, вполне возможно сделать несколько послаблений утверждению Райса для реальных программ, выполняющихся в реальных средах. Во-первых, в теоретической информатике под «программой» подразумевается математическая абстракция, эквивалентная машине Тьюринга (МТ) – самому мощному из вычислительных автоматов. Однако же, в реальных программах далеко не каждый фрагмент их кода эквивалентен МТ. Ниже по иерархии вычислительной мощности находятся линейно-ограниченные, стековые и конечные автоматы. Анализ защищенности двух последних вполне возможен, даже в рамках самой теоретической теории.
Во-вторых, отличительной особенностью МТ является то, что ей доступна память бесконечного размера. Именно из этой особенности вытекает невозможность получить все возможные состояния вычислительного процесса – их попросту бесконечное число. Однако, в реальных компьютерах память далеко не бесконечна. Что еще важнее, в реальных программах число состояний, представляющих интерес с точки зрения задачи анализа защищенности, также конечно (хотя и неприлично велико).
В-третьих, вычисление свойств программы по Райсу, является разрешимой проблемой для ряда малых МТ, имеющих небольшое количество состояний и возможных переходов между ними. Сложно себе представить реальную программу, имеющую от 2 до 4 состояний. Однако, такой фрагмент программы представить себе гораздо легче.
Следовательно, возможен эффективный анализ отдельных фрагментов кода программы, попадающих под перечисленных критерии. На практике, это означает, что:
-
фрагмент кода без циклов и рекурсии может быть всесторонне проанализирован, т.к. эквивалентен конечному автомату;
-
фрагмент с циклами или рекурсией, условие выхода из которых не зависит от входных данных, поддается анализу в качестве конечного или стекового автомата;
-
если условия выхода из цикла или рекурсии зависят от входных данных, длина которых ограничена некоторым разумным порогом, то такой фрагмент в отдельных случаях получится проанализировать как систему линейно-ограниченных автоматов или малых МТ.
А вот все остальное – увы и ах − статическим подходом проанализировать не удастся. Более того, разработка анализатора защищённости исходного кода - это такое направление, работая в котором инженеры ежедневно сталкиваются с трейдофом EXPSPACE <-> EXPTIME, а сводя даже частные случаи к субэкспоненте, радуются как дети, потому что это по-настоящему круто. Подумайте над тем, какова будет мощность множества значений переменной parm1 в последней точке выполнения?
var parm1 = Request.Params["parm1"];
var count = int.Parse(Request.Params["count"]);
for (var i = 0; i < count; i++)
{
i % 2 == 0 ?
parm1 = parm + i.ToString():
parm1 = i.ToString() + parm;
}
Response.Write(parm);
Вот поэтому о теоретических ограничениях можно не особо беспокоиться, поскольку упереться в них на текущих вычислительных мощностях будет крайне затруднительно. Однако же, перечисленные послабления этих ограничений задают правильное направление развития современных статических анализаторов, поэтому иметь в виду их все же стоит.
DAST, IAST и все-все-все
В противовес статическому подходу, работающему с кодом программы без его фактического выполнения, динамический (Dynamic Application Security Testing, DAST) подразумевает наличие развернутой среды выполнения приложения и ее прогон на наиболее интересных с точки зрения анализа наборах входных данных. Упрощая, его можно охарактеризовать, как метод «осознанного научного тыка» («давайте передадим программе вот такие данные, характерные вот для такой атаки и посмотрим, что же из этого выйдет»). Его недостатки очевидны: далеко не всегда есть возможность быстро развернуть анализируемую систему (а зачастую и просто собрать), переход системы в какое-либо состояние может быть следствием обработки предыдущих наборов данных, да и для всестороннего анализа поведения реальной системы количество наборов входных данных должно быть настолько велико, что о его конечности можно рассуждать исключительно теоретически.
Относительно недавно перспективным считался подход, комбинирующий преимущества SAST и DAST – интерактивный анализ (Interactive…, IAST). Отличительной особенностью этого подхода является то, что SAST используется для формирования наборов входных данных и шаблонов ожидаемых результатов, а DAST выполняет тестирование системы на этих наборах, опционально привлекая к процессу человека-оператора в неоднозначных ситуациях. Ирония этого подхода заключается в том, что он вобрал в себя как преимущества, так и недостатки SAST и DAST, что не могло не сказаться на его практической применимости.
Но кто сказал, что в случае динамического анализа нужно выполнять всю программу целиком? Как было показано выше, вполне реально проанализировать значительную часть кода с помощью статического подхода. Что же мешает проанализировать с помощью динамического только оставшиеся фрагменты? Звучит, как план…
А внутре у ней неонка
Существует несколько традиционных подходов к статическому анализу, отличающихся моделью, на основе которой анализатор выводит те или иные свойства исследуемого кода. Самым примитивным и очевидным является сигнатурный поиск, основанный на поиске вхождений какого-либо шаблона в синтаксическую модель представления кода (как правило, это либо поток токенов, либо абстрактное синтаксическое дерево). Отдельные реализации этого подхода используют чуть более сложные модели (семантическое дерево, его отображение на граф отдельных потоков данных и т.п.), но в целом этот подход можно рассматривать исключительно в качестве вспомогательного, позволяющего за линейное время выделить в коде подозрительные места для последующей ручной верификации. Подробнее останавливаться на нём не будем, интересующиеся могут обратиться к посвященной ему серии статей Ивана Кочуркина.
Более сложные подходы оперируют уже моделями выполнения (а не представления или семантики) кода. Такие модели, как правило, позволяют получить ответ на вопрос “может ли контролируемый извне поток данных достичь какой-либо точки выполнения, в которой это приведет к возникновению уязвимости?”. В большинстве случаев, модель здесь представляет собой вариацию на тему графов потока выполнения и потоков данных, либо их комбинацию (например, граф свойств кода). Недостаток подобных подходов также очевиден - в любом нетривиальном коде одного только ответа на этот вопрос недостаточно для успешного детектирования уязвимости. Например, для фрагмента:
var requestParam = Request.Params["param"];
var filteredParam = string.Empty;
foreach(var symbol in requestParam)
{
if (symbol >= 'a' && symbol <= 'z')
{
filteredParam += symbol;
}
}
Response.Write(filteredParam);
такой анализатор выведет из построенной модели утвердительный ответ о достижимости потоком данных Request.Params["param"] точки выполнения Response.Write(filteredParam) и существовании в данной точке уязвимости к XSS. В то время, как на самом деле, данный поток эффективно фильтруется и не может являться носителем вектора атаки. Существует множество способов покрыть частные случаи, связанные с предварительной обработкой потоков данных, но все они в конечном итоге сводятся к разумному балансу между ложными срабатываниями первого и второго типа.

Каким образом можно минимизировать появление ошибок обоих типов? Для этого необходимо учитывать условия достижимости как потенциально уязвимых точек выполнения, так и множеств значений потоков данных, приходящих в такие точки. На основе этой информации становится возможным построить систему уравнений, множество решений которой даст все возможные наборы входных данных, необходимые для того, чтобы прийти в потенциально уязвимую точку программы. Пересечение этого множества со множеством всех возможных векторов атаки, даст множество всех наборов входных данных, приводящих программу в уязвимое состояние. Звучит отлично, но как получить модель, которая содержала бы всю необходимую информацию?
Абстрактная интерпретация и символические вычисления
Допустим, перед нами стоит задача определить, число с каким знаком определяет выражение -42 / 8 * 100500. Самый простой способ - это вычислить данное выражение и убедиться, что получено отрицательное число. Вычисление выражения с вполне определенными значениями всех его аргументов называется конкретным вычислением. Но есть и другой способ решить эту задачу. Давайте на секунду представим, что по какой-то причине у нас нет возможности конкретно вычислить данное выражение. Например, если в него добавилась переменная -42 / 8 * 100500 * x. Определим абстрактную арифметику, в которой результат операций над числами определяется исключительно правилом знака, а значения их аргументов игнорируются:
(+a) = (+)
(-a) = (-)
(-) * (+) = (-)
(-) / (+) = (-)
...
(-) + (+) = (+-)
...
Интерпретируя исходное выражение в рамках данной семантики, получаем: (-) / (+) * (+) * (+) -> (-) * (+) * (+) -> (-) * (+) -> (-). Этот подход будет давать однозначный ответ на поставленную задачу до тех пор, пока в выражении не появятся операции сложения или вычитания. Давайте дополним нашу арифметику таким образом, чтобы значения аргументов операций также учитывались:
(-a) * (+b) = (-c)
(-a) / (+b) = (-c)
...
(-a) + (+b) =
a <= b -> (+)
a > b -> (-)
...
Интерпретируя выражение -42 / 8 * 100500 + x в новой семантике получим результат x >= -527625 -> (+), x < -527625 -> (-).
Описанный выше подход называется абстрактной интерпретацией и формально определяется, как устойчивая аппроксимация семантики выражений, основанная на монотонных функциях над упорядоченными множествами. Говоря более простым языком, это интерпретация выражений без их конкретного вычисления с целью сбора информации в рамках заданного семантического поля. Если мы плавно перейдем от интерпретации отдельных выражений к интерпретации кода программы на каком-либо языке, а в качестве семантического поля определим семантику самого языка, дополненную правилом оперировать всеми входными данными, как неизвестными переменными (символическими значениями), то мы получим подход, именуемый “символическим выполнением” и лежащий в основе большинства перспективных направлений статического анализа кода.
Именно с помощью символических вычислений становится возможным построение контекстного графа символического вычисления (альтернативное название: граф потока вычислений) - модели, всесторонне описывающей процесс вычисления исследуемой программы. Эта модель была рассмотрена в докладе “Автоматическая генерация патчей для исходного кода”, а ее применение для анализа защищенности кода - в статье “Об анализе исходного кода и автоматической генерации эксплоитов”. Вряд ли имеет смысл рассматривать их повторно в рамках данной статьи. Необходимо лишь отметить, что эта модель позволяет получить условия достижимости как любой точки потока выполнения, так и множеств значений всех приходящих в нее аргументов. То есть - именно то, что требуется нам для решения нашей задачи.
Поиск уязвимостей на графе потока вычисления
Формализовав в терминах графа потока вычислений критерии уязвимости к тому или иному классу атак, мы сможем реализовать анализ защищенности кода через разрешение свойств конкретной модели, полученной в результате абстрактной интерпретации исследуемого кода. Например, критерии уязвимости к атакам любых инъекций (SQLi, XSS, XPATHi, Path Traversal и т.п.) можно формализовать примерно так:
Пусть C - граф потока вычисления исследуемого кода.
Пусть pvf(t) - достижимая вершина потока управления на C, являющаяся вызовом функции прямой или косвенной интерпретации текста t, соответствующего формальной грамматике G.
Пусть e - поток аргумента входных данных на С.
Пусть De - множество потоков данных на C, порождаемых от e и достижимых в точке вызова pvf(t).
Тогда приложение уязвимо к атакам инъекции в точке вызова pvf(t), если t принадлежит De и множество значений De включает в себя хотя бы одну пару элементов, при которых, в результате их синтаксического разбора в соответствии с грамматикой G, получаются не изоморфные друг-другу деревья.
Аналогичным образом формализуются уязвимости и к другим классам атак. Однако, здесь необходимо заметить, что не все типы уязвимостей возможно формализовать в рамках какой-либо модели, выводимой только из анализируемого кода. В отдельных случаях может потребоваться дополнительная информация. Например, для формализации уязвимостей к атакам на бизнес-логику, необходимо иметь формализованные правила предметной области приложения, для формализации уязвимостей к атакам на контроль доступа - формализованную политику разграничения доступа и т.п.
Идеальный сферический анализатор защищенности кода в вакууме
Давайте теперь ненадолго отвлечемся от суровой реальности и чуть-чуть помечтаем о том, какой функциональностью должно обладать ядро гипотетического Идеального Анализатора (назовем его условно “IA”)?
Во-первых, оно должно вбирать в себя преимущества SAST и DAST, не включая при этом их недостатки. Из этого в частности следует, что IA должен уметь работать исключительно с имеющимся кодом приложения (исходным или бинарным), не требуя при этом его полноты или развертывания приложения в исполняющей среде. Иными словами, он должен поддерживать анализ проектов с отсутствующими внешними зависимостями или же какими-либо другими факторами, препятствующими сборке и развертыванию приложения. При этом, работа с фрагментами кода, имеющего ссылки на отсутствующие зависимости, должна быть реализована в настолько полной мере, насколько это возможно в каждом конкретном случае. С другой стороны, IA должен уметь эффективно “уворачиваться” не только от теоретических ограничений, накладываемых тьюринговой моделью вычислений, но и осуществлять сканирование за разумное время, потребляя разумное количество памяти и придерживаясь по возможности субэкспоненциальной “весовой категории”.
Во-вторых, вероятность появления ошибок первого рода должна быть сведена к минимуму за счет построения и решения систем логических уравнений и генерации на выходе работающего вектора атаки, позволяющего пользователю подтвердить существование уязвимости одним действием.
В-третьих, IA должен эффективно бороться с ошибками второго рода, предоставляя пользователю возможность ручной проверки всех потенциально уязвимых точек потока выполнения, уязвимость которых сам IA не смог ни подтвердить, ни опровергнуть.
Использование модели, основанной на символических вычислениях, позволяет реализовать все эти требования, что называется “by-design”, за исключением той их части, которая касается теоретических ограничений и субэкспонент. И здесь, как нельзя кстати, придется наш план - использовать динамический анализ там, где не справился статический.
Частичные вычисления, обратные функции и отложенная интерпретация
Представьте себе, что IA содержит в себе некоторую базу знаний, описывающую семантику функций преобразования входных данных, реализованных в стандартной библиотеке языка или исполняющей среды приложения, наиболее популярных фреймворках и CMS. Например, что функции Base64Decode и Base64Encode являются взаимно-обратными, или что каждый вызов StringBuilder.Append добавляет новую строку к уже хранящейся в промежуточной переменной-аккумуляторе этого класса и т.п. Обладая такими знаниями IA будет избавлен от необходимости «проваливаться» в библиотечный код, анализ которого также попадает под все вычислительные ограничения:
// Нужное для выполнения условия значение для cond2 будет выведено солвером на основе информации базы знаний об обратных функциях
if (Encoding.UTF8.GetString(Convert.FromBase64String(cond2)) == "true")
{
var sb = new StringBuilder();
sb.Append(Request.Params["param"]);
// Значение sb.ToString будет получено в результаты эмуляции семантики StringBuilder, описанной в базе знаний библиотечных функций
Response.Write(sb.ToString());
}
Но что делать, если в коде встречается вызов функции, не описанной в базе знаний IA? Давайте представим, что в распоряжении IA есть некая виртуальная среда-песочница, позволяющая запустить произвольный фрагмент анализируемого кода в заданном контексте и получить результат его выполнения. Назовём это “частичным вычислением”. Тогда, перед тем, как честно «провалиться» в неизвестную функцию и начинать её абстрактно интерпретировать, IA может попробовать проделать трюк, называемый «частичным фаззингом». Его общая идея заключается в предварительной подготовке базы знаний по библиотечным трансформирующим функциям и сочетаниям их последовательных вызовов на заранее известных наборах пробных данных. Имея такую базу, можно выполнить неизвестную функцию на тех же наборах данных и сравнить полученные результаты с образцами из базы знаний. Если результаты выполнения неизвестной функции совпадут с результатами выполнения известной цепочки библиотечных функций, то это будет значить, что IA теперь известна семантика неизвестной функции и в ее интерпретации нет необходимости.
Если же для какого-то фрагмента известны множества значений всех потоков данных, приходящих в этот фрагмент, а сам фрагмент не содержит опасных операций, то IA может просто выполнить его на всех возможных потоках данных и использовать полученные результаты вместо абстрактной интерпретации данного фрагмента кода. Причем этот фрагмент может относиться к любому классу вычислительной сложности и это никак не отразится на результатах его выполнения. Более того, даже если множества значений потоков данных, приходящих во фрагмент, заранее неизвестны, IA может отложить интерпретацию этого фрагмента до тех пор, пока не начнется решение уравнения для конкретной опасной операции. На этапе решения на множество значений входных данных накладывается дополнительное ограничение о наличии во входных данных векторов тех или иных атак, что может позволить предположить также и множество значений входных данных, приходящих в отложенный фрагмент и, тем самым, частично вычислить его на данном этапе.
Даже более того, на этапе решения ничего не мешает IA взять конечную формулу достижимости опасной точки и ее аргументов (которую проще всего строить в синтаксисе и семантике того же языка, на котором написан анализируемый код) и “профаззить” ее всеми известными значениями векторов на предмет получения их подмножества, проходящего через все фильтрующие функции формулы:
// Ззначение аргумента Response.Write, проходящее через фильтрующую функцию без изменений, может быть получено в результате фаззинга его формулы постановкой в parm1 значений всех возможных векторов XSS
Response.Write(CustomFilterLibrary.CustomFilter.Filter(parm1));
Описанные выше подходы позволяют справиться с анализом значительной части фрагментов тьюринг-полного кода, но требуют существенной инженерной проработки как в части наполнения базы знаний и оптимизации эмулирования семантики стандартных типов, так и в части реализации песочницы для частичного выполнения кода (никто не захочет, чтобы в процессе анализа внезапно выполнилось что-то вроде File.Delete в цикле), а также поддержки фаззинга n-местных неизвестных функций, интеграции концепции частичного вычисления с SMT-солвером и т.п. Однако же, никаких существенных ограничений на их реализацию нет, в отличии от граблей классического SAST.
Когда гадкий duck-typing становится лебедем
Представьте, что нам необходимо проанализировать следующий код:
var argument = "harmless value";
// UnknownType - тип, объявленный в отсутствующей зависимости
UnknownType.Property1 = parm1;
UnknownType.Property2 = UnknownType.Property1;
if (UnknownType.Property3 == "true")
{
argument = UnknownType.Property2;
}
Response.Write(argument);
Человек без труда увидит здесь достижимую уязвимость к XSS. А вот большинство существующих статических анализаторов ее благополучно прошляпят в связи с тем, что им ничего не известно о типе UnknownType. Однако все, что здесь требуется от IA - это забыть о статической типизации и перейти к утиной. Семантика интерпретации таких конструкций должна полностью зависеть от контекста их использования. Да, интерпретатор ничего не знает о том, чем является UnknownType.Property1 - свойством, полем, или даже делегатом (ссылкой на метод в C#). Но поскольку операции с ней осуществляются как с переменной-мембером какого-то типа, интерпретатору ничего не мешает обрабатывать их именно таким образом. А если, к примеру, далее по коду встретится конструкция UnknownType.Property1(), то ничто не мешает интерпретировать вызов того метода, ссылка на который была ранее присвоена Property1. И так далее, в лучших традициях заводчиков уток-чемпионов.
Подводя итоги
Разумеется, есть масса маркетинговых свистелок, которыми один анализатор якобы выгодно отличается от другого, с точки зрения продающей его стороны. Но, согласитесь, в них нет никакого проку, если ядро продукта не в состоянии обеспечить базовую функциональность, ради которой его и будут использовать. А для того, чтобы её обеспечить, анализатор обязан стремиться по своим возможностям к описанному IA. Иначе ни о какой реальной защищенности на обрабатываемых им проектах и речи быть не может.
Несколько лет назад, один из наших клиентов обратился к нам за проведением анализа защищенности разрабатываемой им системы. В числе вводных данных он предоставил отчет об анализе кода их проекта продуктом, являвшимся на тот момент лидером на рынке SAST-инструментария. Отчет содержал около двух тысяч записей, большинство из которых оказались в итоге на проверку положительно-ложными срабатываниями. Но самым плохим оказалось то, чего не было в отчете. В результате ручного анализа кода, нами были обнаружены десятки уязвимых мест, пропущенных при сканировании. Использование подобных анализаторов приносит больше вреда, чем пользы, как отнимая время, необходимое для разбора всех ложно-положительных результатов, так и создавая иллюзию защищённости из-за ложно-отрицательных. Этот случай, кстати, стал одной из причин разработки нами собственного анализатора.
“Talk is cheap. Show me the code.”
Было бы странным не завершить статью небольшим примером кода, позволяющим проверить степень идеальности того или иного анализатора на практике. Voila - ниже представлен код, включающий в себя все базовые кейсы, покрываемые описанным подходом к абстрактной интерпретации, но не покрываемые более примитивными подходами. Каждый кейс реализован настолько тривиально, насколько это возможно и с минимальным количеством инструкций языка. Это пример для C#/ASP.Net WebForms, но не содержит какой-либо специфики и легко может быть транслирован в код на любом другом ООП-языке и под любой web-фреймворк.
var parm1 = Request.Params["parm1"];
const string cond1 = "ZmFsc2U="; // "false" в base64-кодировке
Action<string> pvo = Response.Write;
// False-negative
// Анализаторы, не интерпретирующие поток выполнения по потокам данных функционального типа, не сообщат здесь об уязвимости
pvo(parm1);
// Для анализаторов, требующих компилируемый код, этот фрагмент необходимо удалить
#region
var argument = "harmless value";
UnknownType.Property1 = parm1;
UnknownType.Property2 = UnknownType.Property1;
UnknownType.Property3 = cond1;
if (UnknownType.Property3 == null)
{
argument = UnknownType.Property2;
}
// False-positive
// Анализаторы, игнорирующие некомпилируемый код, сообщат здесь об уязвимости
Response.Write(argument);
#endregion
// False-positive
// Анализаторы, не учитывающие условия достижимости точек выполнения, сообщат здесь об уязвимости
if (cond1 == null) { Response.Write(parm1); }
// False-positive
// Анализаторы, не учитывающие семантику стандартных фильтрующих функций, сообщат здесь об уязвимости
Response.Write(WebUtility.HtmlEncode(parm1));
// False-positive
// Анализаторы, не учитывающие семантику нестандартных фильтрующих функций, сообщат здесь об уязвимости
// (CustomFilter.Filter реализует логику `s.Replace("<", string.Empty).Replace(">", string.Empty)`)
Response.Write(CustomFilterLibrary.CustomFilter.Filter(parm1));
if (Encoding.UTF8.GetString(Convert.FromBase64String(cond1)) == "true")
{
// False-positive
// Анализаторы, не учитывающие семантику стандартных кодирующих функций, сообщат здесь об уязвимости
Response.Write(parm1);
}
var sum = 0;
for (var i = 0; i < 10; i++)
{
for (var j = 0; j < 15; j++)
{
sum += i + j;
}
}
if (sum != 1725)
{
// False-positive
// Анализаторы, аппроксимирующие или игнорирующие интерпретацию циклов, сообщат здесь об уязвимости
Response.Write(parm1);
}
var sb = new StringBuilder();
sb.Append(cond1);
if (sb.ToString() == "true")
{
// False-positive
// Анализаторы, не интерпретирующие семантику типов стандартной библиотеки, сообщат здесь об уязвимости
Response.Write(parm1);
}
Результатом анализа данного кода должно являться сообщение о единственной уязвимости к атакам XSS в выражении pvo(parm1).
Вступить и компилировать с готовым к сканированию проектом можно здесь.
Но, как говорится, “лучше один раз увидеть…” и, в первую очередь, мы проверили на соответствие IA разрабатываемый нами анализатор, по чистой случайности называющийся AI:
А вы - уже проверили свой? ;)
На правах бонуса для дочитавших до конца
Мы открываем публичное альфа-тестирование бесплатной утилиты Approof. В нее не включена функциональность анализа кода и не используется весь описанный выше матастафический хардкор, зато включена функциональность выявления в проектах уязвимых внешних компонентов, недостатков конфигурации, чувствительных к разглашению данных, а также внедренных веб-шеллов и вредоносного кода:
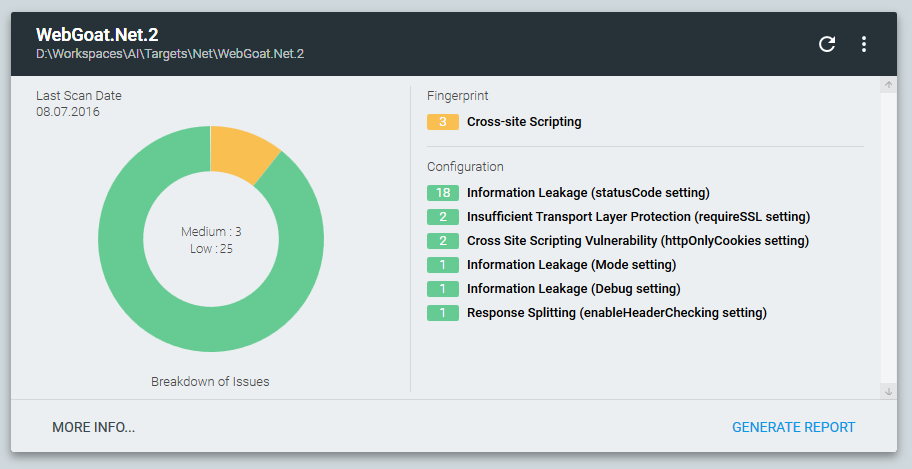
Скачать утилиту можно на официальном сайте. Перед ее использованием обязательно ознакомьтесь с лицензионным соглашением. В ходе анализа, Approof собирает неконфиденциальную статистику по проекту (CLOC, типы файлов, используемые фреймворки и т.к.) и, опционально, отправляет ее на сервер PT. Отключить отправку статистики или ознакомиться с сырым json, содержащим собранные данные, можно в разделе About приложения.

Комментарии
comments powered by Disqus