It would not be a big overstatement to say that the SAST market is currently booming. Research papers on SAST are published at least once every two months, new SAST tools become available every year, and whole sections at international information security conferences are dedicated to SAST’s role in software development. SAST tool vendors constantly bombard the prospective users with tons of information about their products, and it is not easy to understand which part of it is true, and which is just a marketing hype. Let’s try to understand the real capabilities of such tools, and what we should do if they cannot handle some issues. We are going to take a little dive into the theory that lies in the basis of state-of-the-art SAST tools.
Turing, Rice and all, all, all
TL/DR: The problem of static application security testing is algorithmically undecidable.
Imagine a set of fully abstract programs (let’s call it P) that always hang on some inputs and halt after doing some operations on other inputs. Obviously, class P includes all theoretically possible programs, because each of them has this property.
Now imagine that one of these programs is a code analyzer (let’s call it h) that can answer this simple question: Does an arbitrary program p of P hang on the given input n? Obviously, h can answer this question only if it completes its job; by doing that, it tells us that p hangs on n. In other words, if p(n) doesn’t halt, then h(p(n)) must complete its job in a finite number of steps; and if p(n) halts, then h(p(n)) must hang.
Now imagine what happens if we try using that analyzer to answer this question: Will the analyzer hang if it tries to analyze itself analyzing itself? (Because p can be any program of P, so it can be h, too.) But in this case, if h(h(n)) halts, then the analyzing of h(n) hangs; and if h(h(n))) hangs, then the analyzing of h(n) halts. But h is h(n), so we have a contradiction, which means that an h-like analyzer cannot exist.
The above is a loose summary of the proof of The Halting Theorem that was formulated by Alan Turing, the founder of the modern theoretical computer science, in 1936. The theorem states that there is no program able to analyze another program and answer the question whether that program would halt on a certain input. Well, maybe we could create a program that can answer the question about some other properties of programs under examination?
Because set P includes all possible programs, we can always split it into two classes (let’s call them A and B) based on the existence of any nontrivial, invariant property in the programs. Here nontriviality and invariance means that any program of P either has that property or doesn’t have it. Moreover, either all functionally identical programs (which produce the same outputs when fed identical inputs) have that property, or none of them has it.
Imagine that there exists a code analyzer (let’s call it q) that takes an arbitrary program p of P as an input, and halts if p belongs to one of the classes (A or B). For example, let it be class A. Let pa be a program that belongs to class A and gets caught in an endless loop on any input. Let’s also take an arbitrary program (pb) from class B. For each program p, let’s define program p’ that takes input x and executes the following algorithm:
- p(p)
- pb(x)
Now let’s create program q’ that takes an arbitrary program p as an input, creates for it p’, and calculates q(p’).
If p’ hangs on the first step, it means that p’ is functionally identical to pa (and belongs to class A), so q’ must halt immediately. If p’ completes the first step, it means that p’ is functionally identical to pb (and belongs to class B), so q’ must hang. Therefore, for any program p, q’(p) halts if p(p) doesn’t halt. But q’ can take the place of p, so p(p) halts only if p(p) doesn’t halt. Again, it is a contradiction.
The statement that there is no program that can answer the question whether an arbitrary program has any nontrivial, invariant properties was proved by the scientist Henry Gordon Rice in 1953. Basically, his research has generalized the Halting Theorem, because the property of halting on a given input is nontrivial and invariant. Depending on the properties considered, Rice’s theorem has infinitely many practical values: “It is impossible to use a program to classify an algorithm implemented by another program,” “It is impossible to use a program to prove that two other programs implement one and the same algorithm,” “It is impossible to use a program to prove that another program doesn’t enter certain states on any inputs,” etc. We should consider the last example in more detail.
When any (abstract or real) algorithm is being executed by a universal executing program (for example, by a virtual machine that emulates a real computer with its operating system), we can take a snapshot of that virtual machine, including the state of the application (algorithm) being executed in the address space of the virtual machine and its external environment, such as disk drives, the state of external devices, etc. Later we can restore that state from the snapshot and continue running the application from the very same point. In essence, the whole process of any program’s execution is a sequence of changing states that is determined by the program’s source code. If there are any errors in the configuration or implementation of the program or the virtual machine, it is highly probable that the control flow will enter a state that has never been intended by the program’s developer.
What is a vulnerability? It is an opportunity of using input data to make the control flow enter a state that allows the attacker to realize a threat regarding the data being processed by the program. Therefore, we can define the security of any program as its ability to always remain within the predetermined set of admissible states that determine its security policy, regardless of the initial input. In that case, the security analysis problem boils down to checking whether it is impossible for the program to enter any state not allowed by the security policy on an arbitrary input. That is, to the problem whose algorithmic undecidability has been long ago proved by Henry Rice.
Does it mean that the whole SAST market is basically a snake oil industry? In theory – yes, it is. But in practice, as usually, the answer to that question is not that simple.
SAST theory in practice
Even as pure theorists, we could ease some requirements of Rice’s statement for real programs executed in real environments. First, in theoretical computer science, a program is a mathematical abstraction that is equivalent to a Turing machine (TM), the most powerful computing automaton. However, in real programs only some code fragments are truly equivalent to TM. In terms of computation power, linear bounded automata, stack machines, and finite state machines are below TM. Even as pure theorists, we can analyze the security of stack machines and finite state machines.
Second, TM’s distinguishing feature is that it can use a memory of an infinite size. This feature is the reason why we cannot get all possible states of a computation process – simply because there are an infinite number of them. But the amount of memory in real computers is far from infinite. What is even more important, in real programs the number of states that may be of some interest from the viewpoint of security analysis is also finite, though obscenely huge.
Third, calculating a program’s properties based on Rice’s statement is a decidable problem for a number of small TMs that have few states and few possible transitions between them. It is hard to imagine a real program that has 2 to 4 states. But it is much easier to imagine a program’s fragment with that number of states.
Therefore, we can effectively analyze code fragments that meet the above criteria. In practice it means that:
-
We can thoroughly analyze a code fragment without any program loops or recursion, because it is equivalent to a finite state machine;
-
We can analyze a code fragment with some program loops or recursion if the exit conditions do not depend on input, by considering it as a finite state machine or a stack machine;
-
If the exit conditions for the program loop or recursion depends on input whose length is reasonably limited, in some cases we can analyze the fragment as a system of linear bounded automata or a system of small TMs.
As for other code fragment types, alas, we cannot use the static approach to analyze them. Moreover, when developing source code security analyzers, software engineers have to trade off between EXPSPACE and EXPTIME on a daily basis. When they do manage to reduce even special cases to a sub-exponential algorithm, they feel happy like little kids, because it’s really awesome! How do you think, what will be the power of the set of possible values of variable parm1 at the last execution point?
var parm1 = Request.Params["parm1"];
var count = int.Parse(Request.Params["count"]);
for (var i = 0; i < count; i++)
{
i % 2 == 0 ?
parm1 = parm + i.ToString():
parm1 = i.ToString() + parm;
}
Response.Write(parm);
That’s why we don’t have to worry too much about the theoretical limitations, because it is extremely unlikely that we would ever hit them when using any practically available computation power. However, the easing of the requirements has set the evolution of modern static code analyzers on the right course, so we should keep it in mind anyway.
DAST, IAST, and all, all, all
Unlike the static approach, where program code is analyzed without actually being executed, the dynamic approach (Dynamic Application Security Testing, DAST) requires having a runtime environment and executing the program on some inputs that are most useful for analysis purposes. Simply speaking, we can call DAST a “method of informed trial and error”: “Let’s feed these input data, which are characteristic for that kind of attack, to the program and see what happens.” This method has obvious drawbacks: In many cases we can’t quickly deploy the system to be analyzed (sometimes we can’t even build it), the system’s transition to a certain state may be the result of processing the previous inputs, and a comprehensive analysis of a real system’s behavior requires feeding it so many inputs that it is utterly impractical to try testing the system on each of them.
Not long ago, Interactive Application Security Testing (IAST) – an approach that combined the strengths of SAST and DAST – was considered promising. IAST’s distinctive feature is that the SAST part generates inputs and the templates of expected results, and the DAST part tests the system on these inputs, prompting the human operator to interfere in ambiguous situations. The irony of this approach is that it has inherited both strengths and weaknesses of SAST and DAST, which calls in question its practicality.
But who said that dynamic code analysis means that we have to execute the whole program? As we have already seen, we can use the static approach to analyze a major portion of the program’s code. Why can’t we use the dynamic approach to analyze only the remaining code fragments? It sounds like we have a plan…
Mumbo Jumbo™ Inside
There are several classic approaches to static code analysis, which use different models for producing the properties of the code under examination. The most primitive and obvious approach is signature search. It is based on looking for occurrences of some template in the syntax code presentation model (which is usually a token flow or an abstract syntax tree). Some implementations of that approach use slightly more-complex models (semantic tree, its mapping to the graph of some data flow, etc.). But on the whole, this approach is only useful as a secondary one: It allows us to mark suspicious parts of the code within a linear time, so that later we can check them manually. Enough said about this approach; if you are interested in it, please read the series of articles by Ivan Kochurkin.
More-complex approaches use code execution (not presentation or semantic) models. Such models usually can answer this question: Can a data flow under external control reach such an control flow point that it creates a vulnerability? In most cases, the model is a control flow graph or a data flow diagram, or a combination of them (for example, a code property graph). Such approaches have an obvious drawback: When analyzing any nontrivial code, answering the above question is not enough to successfully detect a vulnerability. For example, here’s a code fragment:
var requestParam = Request.Params["param"];
var filteredParam = string.Empty;
foreach(var symbol in requestParam)
{
if (symbol >= 'a' && symbol <= 'z')
{
filteredParam += symbol;
}
}
Response.Write(filteredParam);
Based on the created model, the trivial graph-based analyzer will confirm that the data flow Request.Params["param"] can reach the control flow point Response.Write(filteredParam), and that there is a vulnerability to XSS attacks there. Actually, that data flow is effectively filtered and cannot carry the attack vector! There are many methods that allow us to cover special cases associated with data flow preprocessing, but ultimately each of them means finding a reasonable balance between false positives and false negatives, also known as Type I errors and type II errors.

How can we minimize the number of errors of both types? We need to consider reachability conditions both for potentially vulnerable control flow points and for combinations of values of the data flows that can reach those points. Based on that information, we can create a system of equations whose set of solutions will give us all possible inputs that are necessary to reach the potentially vulnerable point in the program. The intersection of this set with the set of all possible attack vectors will produce the set of all inputs that bring the program to a vulnerable state. It sounds great, but how can we build a model that contains all necessary information?
Abstract interpretation and symbolic computation
Suppose, we need to find out the sign of the number produced by this expression: -42 / 8 * 100500. The simplest way to do it is to calculate the result and check if it is negative. The computation of an expression by using specific values of all arguments is known as “concrete computation.” But we can also solve this problem in a different way. Imagine that for some reason the concrete computation of this expression cannot be done. For example, because a variable has been added: -42 / 8 * 100500 * x. Let’s define an abstract arithmetic in which the result of operations on numbers is defined only by the signs, while the absolute values of all arguments are ignored:
(+a) = (+)
(-a) = (-)
(-) * (+) = (-)
(-) / (+) = (-)
...
(-) + (+) = (+-)
...
Let’s interpret the initial expression within this semantics: (-) / (+) * (+) * (+) -> (-) * (+) * (+) -> (-) * (+) -> (-). This approach will give an unambiguous answer to the question as long as the expression does not contain any addition or subtraction operators. Let’s modify our arithmetic to consider the absolute values of arguments, too:
(-a) * (+b) = (-c)
(-a) / (+b) = (-c)
...
(-a) + (+b) =
a <= b -> (+)
a > b -> (-)
...
If we interpret the expression -42 / 8 * 100500 + x based on the new semantics, the result will be x >= -527625 -> (+), x < -527625 -> (-).
The above approach is called abstract interpretation. It is formally defined as a stable approximation of the semantics of expressions, based on monotonic functions over ordered sets. Simply speaking, it is an interpretation of expressions without a concrete computation of them, intended to gather information within the given semantic field. Let’s smoothly go from interpreting some expressions to interpreting program code in some programming language. As for the semantic field, let’s define the semantics of the language, complemented with the rule to handle all inputs as unknown variables (symbolic values). The result is an approach known as “[symbolic execution,]”(https://en.wikipedia.org/wiki/Symbolic_execution) which lies in the basis of most promising SAST tools.
It is symbolic computation that allows us to create a context graph for symbolic computation (also known as a computation flow graph). It is a model that comprehensively describes the computation process of the program under examination. That model was considered in the report “Automated generation of source code patches”, and the model’s application for code security analysis was covered in the article “Source Code Security Assessment and Automatic Exploit Generation” (p. 23-24). It doesn’t make much sense for us to cover them again in this article. It should be noted that the model allows us to get reachability conditions both for any control flow point and for sets of values of input arguments. That is, it is just what we need to solve our problem.
Vulnerability search based on the computation flow graph
If we formalize vulnerability criteria to a certain attack class in terms of the computation flow graph, we can implement code security analysis by finding out the properties of a concrete model obtained as a result of the abstract interpretation of the code under examination. For example, we can formalize the criteria of vulnerability to any injection attacks (SQLi, XSS, XPATHi, Path Traversal, etc.) as follows:
Let C be the computation flow graph of the code under examination.
Let pvf(t) be the reachable control flow node in C, so that pvf(t) is the call of the function of direct or indirect interpretation of text t that conforms to formal grammar G.
Let e be the input data argument flow in С.
Let De be the set of data flows in C that are derived from e and reachable at the pvf(t) invocation point.
Then the program is vulnerable to injection attacks at the pvf(t) invocation point if t belongs to De and the set of values of De includes at least one pair of elements which, if syntactically parsed in conformance with grammar G, produces trees that are not isomorphic to each other.
We can formalize vulnerabilities to other attack classes in a similar manner. However, it should be noted that not all vulnerability types can be formalized within a model created based on the code under examination. In some cases, we may need more information. For example, to formalize vulnerabilities to attacks against business logic, we need to have formalized rules for the program’s application domain; to formalize vulnerabilities to attacks against access control, we need formalized access control policies; etc.
Ideal – that is, purely theoretical – code security analyzer
Let’s forget about the harsh reality for awhile and try answering this question: If a hypothetical Ideal Analyzer (IA) could exist, what functionality should it have?
First, it should have the strengths of both SAST and DAST, but do not have their weaknesses. Among other things, it means that IA should be able to analyze any existing program code (source code or binary code) without requiring its completeness or the program to be deployed in the runtime environment. In other words, IA should be able to analyze projects with missing external dependencies, or when some other factors do not let us to build or deploy the program. Moreover, handling code fragments that contain references to missing dependencies should be implemented as completely as possible in each particular case. On the other hand, IA should not only be able to avoid the theoretical limitations imposed by the Turing computation model, but also complete scanning within a reasonable time, consume a reasonable amount of memory, and, when possible, stay in the sub-exponential “weight category.”
Second, the probability of Type I errors should be minimized by creating and solving systems of logical equations and generating a working attack vector that allows the user to confirm the existence of the vulnerability in one click.
Third, IA should effectively deal with Type II errors by allowing the user to check all potentially vulnerable control flow points manually if IA was unable to either prove or disprove their vulnerability.
Using a model based on symbolic computation allows us to implement all of the above requirements by-design, except for the ones related to theoretical limitations and sub-exponentiality. Our plan – to employ dynamic code analysis when static code analysis fails – is just what we need!
Partial computation, inverse functions, and deferred interpretation
Imagine that IA contains a knowledge base that describes the semantics of input transformation functions implemented in the standard language library or the program’s runtime environment, in the most popular frameworks and CMSs. For example, imagine that the functions Base64Decode and Base64Encode are mutually inverse, or that each call of StringBuilder.Append adds a new line to the string already stored in the temporary variable of that class, etc. Thanks to all that knowledge, IA doesn’t have to “fall through” into the library code whose analysis is subject to all computational limitations, too:
// The value of cond2 required for meeting the condition will be produced by the solver based on the knowledge base on inverse functions
if (Encoding.UTF8.GetString(Convert.FromBase64String(cond2)) == "true")
{
var sb = new StringBuilder();
sb.Append(Request.Params["param"]);
// The value of sb.ToString will be obtained by emulating the semantics of StringBuilder described in the knowledge base on library functions
Response.Write(sb.ToString());
}
But what if there is a call of a function in the code, but there is no description of that function in the IA knowledge base? Imagine that IA can use a virtual sandbox environment that allows it to run an arbitrary fragment of the code under examination in the given context and get the result of its execution. Let’s call it “partial computation.” In that case, before “falling through” into an unknown function and starting to interpret it abstractly, IA can try doing a trick called “partial fuzzing.” The general idea of that trick is that we can prebuild a knowledge base on library transformation functions and any combinations of sequential calls of such functions based on the already-known combinations of test data. Having that knowledge base, we can execute an unknown function on the same combinations of data and then compare the results to the samples from the knowledge base. If the results of executing the unknown function match the results of executing a known sequence of library functions, it would mean that now IA knows the semantics of the unknown function, so there is no need to interpret the function.
But if the set of input values of all data flows are known for a code fragment that doesn’t contain any dangerous operators, IA can simply execute that fragment on all possible data flows and use the results instead of abstractly interpreting that fragment. That fragment can be of any computation power class, without any impact whatsoever on the results of its execution. Moreover, even if we do not know beforehand the the set of input values of data flows for a code fragment, IA can defer the interpretation of that fragment until it starts to solve the equation for the specific dangerous operator. At the solution step, an additional limitation about the presence of specific attack vectors in input data is imposed on the set of input values, which may allow us to make assumptions about the set of input values for the deferred fragment, and thereby partially compute it at this step.
Moreover, at the solution step, IA can simply take the final reachability formula for the dangerous point and its arguments (it would be easier to build the formula by using the syntax and semantics of the language used in the code under examination) and fuzzy it thoroughly on all known vector values to get their subset that can pass through all filter functions of the formula:
// The value of the Response.Write argument that passes unchanged through the filter function can be obtained by fuzzing its formula by substituting the values of all possible XSS vectors in parm1
Response.Write(CustomFilterLibrary.CustomFilter.Filter(parm1));
The above approaches allow us to analyze a good share of Turing-complete code fragments but require significant efforts by the software engineers, who need to build knowledge bases and optimize the emulation of semantics of standard types, and to implement the sandbox for partial code execution (surely nobody wants for something like File.Delete to be executed in program loop during the analysis). The engineers also need to provide support for fuzzing of n-local unknown functions, integrate the concept of partial execution with the SMT solver, etc. Nevertheless, there are no substantial limitations to doing all these things, quite unlike the drawbacks of the classic SAST.
When the ugly duck-typing becomes a swan
Imagine that we need to analyze the following code:
var argument = "harmless value";
// UnknownType - a type that is declared in a missing dependency
UnknownType.Property1 = parm1;
UnknownType.Property2 = UnknownType.Property1;
if (UnknownType.Property3 == "true")
{
argument = UnknownType.Property2;
}
Response.Write(argument);
A human can easily detect a reachable XSS vulnerability in the above code fragment. However, the majority of the existing static code analyzers will miss it simply because they don’t know anything about the UnknownType type. But IA only needs to forget about static typing and use duck typing instead. The semantics of interpretation of such constructs should be completely dependent on the context of their use. Yes, the interpreter doesn’t know what UnknownType.Property1 is – a property, a field, or even a delegate (a reference to a method in C#). But because operations on it are done as if it is a variable-member of a specific type, the interpreter can simply process it in the respective manner. And if, for example, IA finds the construct UnknownType.Property1() further in the code, it can simply interpret the call of the method, a reference to which has been earlier attributed to Property1. Etcetera, etcetera, in keeping with the best traditions of duck breeders.
Taking stock
Surely, there are tons of bells and whistles which supposedly make one code analyzer better than another, at least from the vendor’s viewpoint. But if the analyzer’s engine cannot provide even the basic functionality, what’s the point of having lots of trendy features? To make the users happy, the analyzer’s developers must strive to provide the functionality that is as close to that of the IA as possible. Otherwise, you can just forget about any actual security of the projects checked by the analyzer.
Some years ago, a customer of ours asked us to analyze the security of a system he was developing. Among the introductory data, he enclosed a report of code analysis done by an analyzing product that was the leader of the SAST tools market at that time. The report contained about two thousand entries, most of which eventually proved to be false positives. But the worst part was what was missing in the report. By manually analyzing the code, we have found dozens of vulnerable points that had been missed by the leading analyzer! So using such analyzers does more harm than good: You waste your time on manually checking all false positives, and the presence of false negatives creates an illusion of security. By the way, that case was one of the reasons why we’ve decided to develop our own analyzer.
“Talk is cheap. Show me the code.”
It would be amiss not to complete the article with a small code sample that allows you to check the “degree of ideality” of any analyzer in practice. Presto! Below you can see the code that includes all basic cases covered by the approach to abstract interpretation described in this article, but not covered by the more-primitive approaches. Each case has been implemented as trivially as possible and contains few instructions. Though the example is intended for C#/ASP.Net WebForms, it does not contain any specifics and can be easily translated into any other OOP code or adapted for any Web framework.
var parm1 = Request.Params["parm1"];
const string cond1 = "ZmFsc2U="; // "false" in base64
Action<string> pvo = Response.Write;
// False-negative
// An analyzer that doesn’t interpret the control flow by functional data flows will not report a vulnerability here
pvo(parm1);
// If the analyzer requires compiled code, delete this fragment
#region
var argument = "harmless value";
UnknownType.Property1 = parm1;
UnknownType.Property2 = UnknownType.Property1;
UnknownType.Property3 = cond1;
if (UnknownType.Property3 == null)
{
argument = UnknownType.Property2;
}
// False-positive
// An analyzer that ignores noncompiled code will report a vulnerability here
Response.Write(argument);
#endregion
// False-positive
// An analyzer that ignores execution point reachability conditions will report a vulnerability here
if (cond1 == null) { Response.Write(parm1); }
// False-positive
// An analyzer that ignores the semantics of standard filter functions will report a vulnerability here
Response.Write(WebUtility.HtmlEncode(parm1));
// False-positive
// An analyzer that ignores the semantics of nonstandard filter functions will report a vulnerability here
// (CustomFilter.Filter implements the logic of `s.Replace("<", string.Empty).Replace(">", string.Empty)`)
Response.Write(CustomFilterLibrary.CustomFilter.Filter(parm1));
if (Encoding.UTF8.GetString(Convert.FromBase64String(cond1)) == "true")
{
// False-positive
// An analyzer that ignores the semantics of standard encoding functions will report a vulnerability here
Response.Write(parm1);
}
var sum = 0;
for (var i = 0; i < 10; i++)
{
for (var j = 0; j < 15; j++)
{
sum += i + j;
}
}
if (sum != 1725)
{
// False-positive
// An analyzer that approximates or ignores the interpretation of program loops will report a vulnerability here
Response.Write(parm1);
}
var sb = new StringBuilder();
sb.Append(cond1);
if (sb.ToString() == "true")
{
// False-positive
// An analyzer that does not interpret the semantics of standard library types will report a vulnerability here
Response.Write(parm1);
}
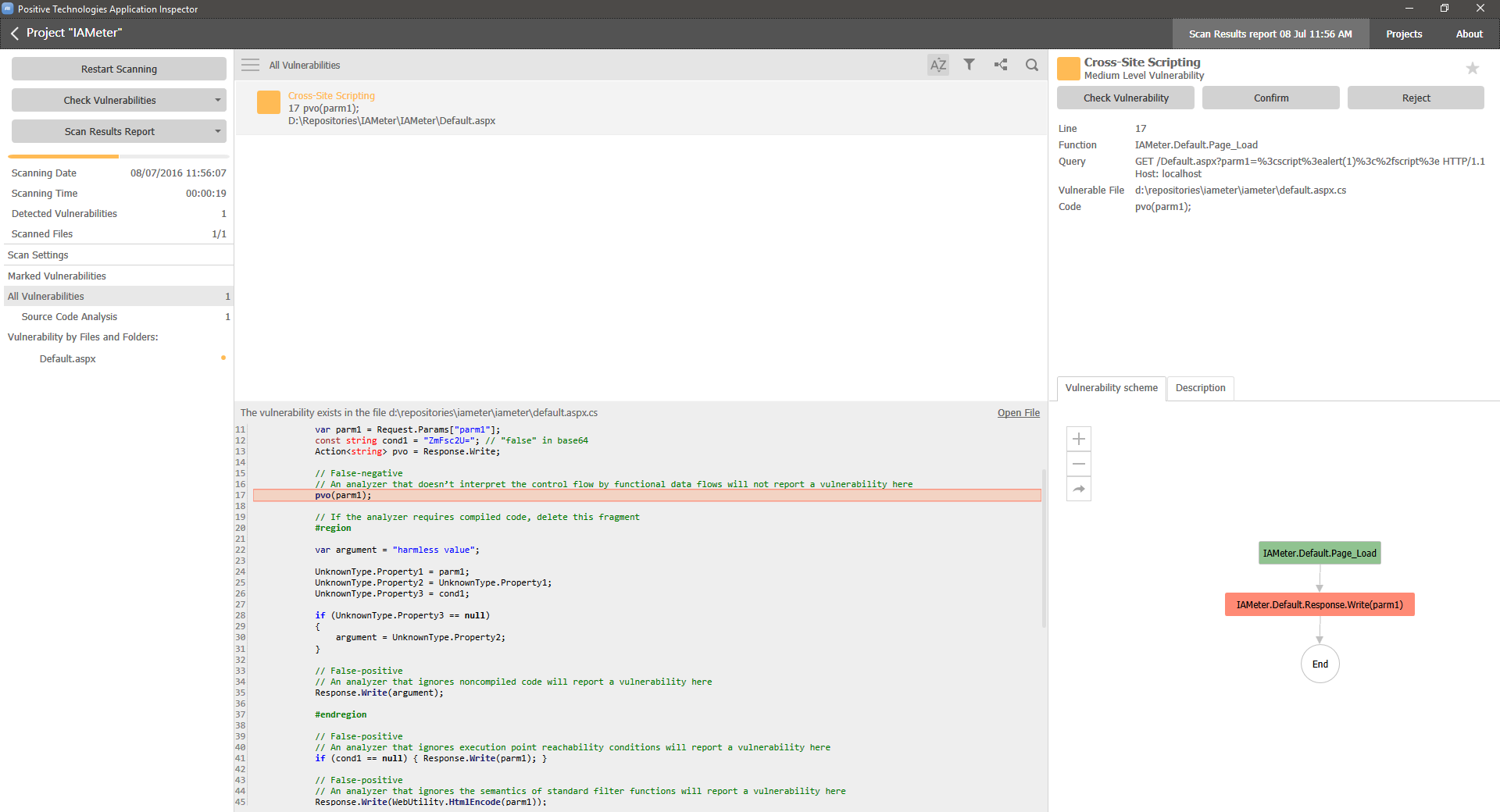
The result of analyzing this code should be a report of a single vulnerability to XSS attacks in the expression pvo(parm1).
You can join us and compile a ready-to-scan project here
But, as the saying goes, a picture is worth a thousand words. So we checked our own analyzer, coincidentally called AI, on conformance to IA:
Have you already checked your analyzer? ;)
A little bonus for the most patient reader
Welcome to the public alpha test of our freeware tool Approof! It doesn’t include the code analysis functionality and doesn’t implement all of the above semitheoretical stuff. Nonetheless, Approof can detect vulnerable external components, configuration defects, and sensible information, as well as injected web shells and malware:
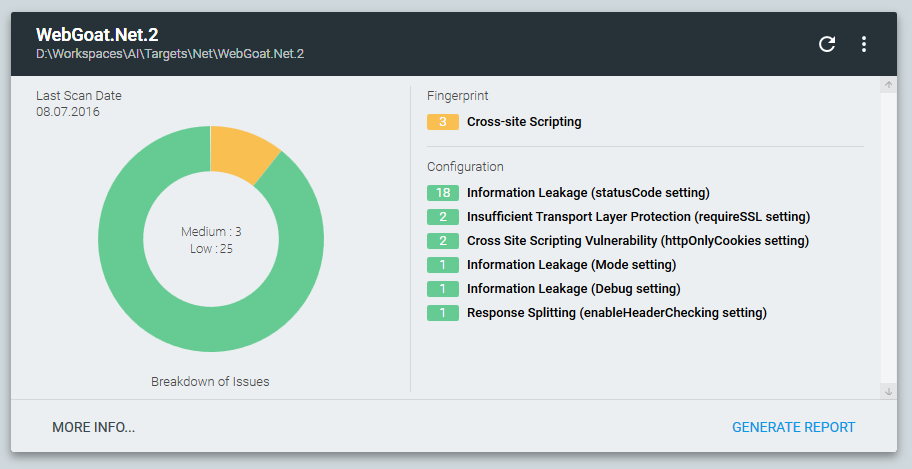
You can download Approof from our official website. Before using the tool, please read the license agreement. When analyzing code, Approof collects nonconfidential statistics on the project (CLOC, file types, frameworks used, etc.) and optionally sends it to the PT server. You can turn off the sending of statistics or take a look at the raw json that contains the collected data via the tool’s About menu.
Комментарии
comments powered by Disqus